• Lack Of Randomness In The Key Generation Process Video
• Lack Of Randomness In The Key Generation Process 2
• Lack Of Randomness In The Key Generation Process Theory

• Cryptography Tutorial

• Cryptography Useful Resources

• Selected Reading

The Data Encryption Standard (DES) is a symmetric-key block cipher published by the National Institute of Standards and Technology (NIST).

DES is an implementation of a Feistel Cipher. It uses 16 round Feistel structure. The block size is 64-bit. Though, key length is 64-bit, DES has an effective key length of 56 bits, since 8 of the 64 bits of the key are not used by the encryption algorithm (function as check bits only). General Structure of DES is depicted in the following illustration −

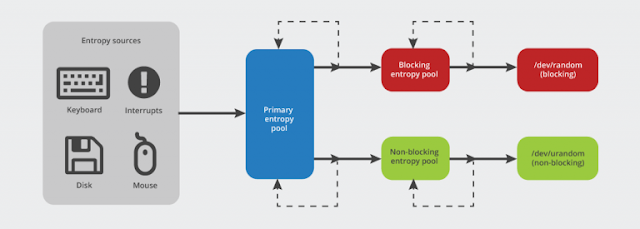
In the common parlance, randomness is the apparent lack of pattern or predictability in events. A random sequence of events, symbols or steps often has no order and does not follow an intelligible pattern or combination. Individual random events are by definition unpredictable, but since they often follow a probability distribution, the frequency of different outcomes over numerous events is predictable. For example, when throwing two dice, the outcome of any particular roll is unpredictable, bu. RFC 4086 Randomness Requirements for Security June 2005 While the above analysis is correct on average, it can be misleading in some cases for cryptographic analysis where what is really important is the work factor for an adversary. For example, assume that there is a pseudo-random number generator generating 128-bit keys, as in the previous paragraph, but that it generates zero half of the. Being truly random is necessary in certain situations; for example during part of a key exchange protocol, where a permanent master key is used to encrypt less expensive session keys to send over. If the process of key generation were to be 'deterministic', an adversary could otherwise guess the next session key that we'll use, or perhaps even. Ideally, the key must be completely random; if the key is, say, a 128-bit key, the random number generator must have 128 bits of entropy available. Human movements are somewhat predictable (you aren't going to move the mouse two meters left), but the more you move, the more entropy you feed into the pool.

Since DES is based on the Feistel Cipher, all that is required to specify DES is −

• Round function
• Key schedule
• Any additional processing − Initial and final permutation

Initial and Final Permutation

The initial and final permutations are straight Permutation boxes (P-boxes) that are inverses of each other. They have no cryptography significance in DES. The initial and final permutations are shown as follows −

Round Function

The heart of this cipher is the DES function, f. The DES function applies a 48-bit key to the rightmost 32 bits to produce a 32-bit output.

• Expansion Permutation Box − Since right input is 32-bit and round key is a 48-bit, we first need to expand right input to 48 bits. Permutation logic is graphically depicted in the following illustration −

• The graphically depicted permutation logic is generally described as table in DES specification illustrated as shown −

• XOR (Whitener). − After the expansion permutation, DES does XOR operation on the expanded right section and the round key. The round key is used only in this operation.

• Substitution Boxes. − The S-boxes carry out the real mixing (confusion). DES uses 8 S-boxes, each with a 6-bit input and a 4-bit output. Refer the following illustration −

• The S-box rule is illustrated below −

• There are a total of eight S-box tables. The output of all eight s-boxes is then combined in to 32 bit section.

• Straight Permutation − The 32 bit output of S-boxes is then subjected to the straight permutation with rule shown in the following illustration:

Key Generation

The round-key generator creates sixteen 48-bit keys out of a 56-bit cipher key. The process of key generation is depicted in the following illustration −

The logic for Parity drop, shifting, and Compression P-box is given in the DES description.

DES Analysis

The DES satisfies both the desired properties of block cipher. These two properties make cipher very strong.

• Avalanche effect − A small change in plaintext results in the very great change in the ciphertext.

• Completeness − Each bit of ciphertext depends on many bits of plaintext.

During the last few years, cryptanalysis have found some weaknesses in DES when key selected are weak keys. These keys shall be avoided. Wpa psk raw key generator.

DES has proved to be a very well designed block cipher. There have been no significant cryptanalytic attacks on DES other than exhaustive key search.

Symmetric-key algorithms^[a] are algorithms for cryptography that use the same cryptographic keys for both encryption of plaintext and decryption of ciphertext. The keys may be identical or there may be a simple transformation to go between the two keys.^[1] The keys, in practice, represent a shared secret between two or more parties that can be used to maintain a private information link.^[2] This requirement that both parties have access to the secret key is one of the main drawbacks of symmetric key encryption, in comparison to public-key encryption (also known as asymmetric key encryption).^[3][4]

Types[edit]

Symmetric-key encryption can use either stream ciphers or block ciphers.^[5]

• Stream ciphers encrypt the digits (typically bytes), or letters (in substitution ciphers) of a message one at a time. An example is the Vigenère Cipher.
• Block ciphers take a number of bits and encrypt them as a single unit, padding the plaintext so that it is a multiple of the block size. Blocks of 64 bits were commonly used. The Advanced Encryption Standard (AES) algorithm approved by NIST in December 2001, and the GCM block cipher mode of operation use 128-bit blocks.

Implementations[edit]

Lack Of Randomness In The Key Generation Process Video

Examples of popular symmetric-key algorithms include Twofish, Serpent, AES (Rijndael), Blowfish, CAST5, Kuznyechik, RC4, DES, 3DES, Skipjack, Safer+/++ (Bluetooth), and IDEA.^[6]

Cryptographic primitives based on symmetric ciphers[edit]

Symmetric ciphers are commonly used to achieve other cryptographic primitives than just encryption.^{[citation needed]}

Encrypting a message does not guarantee that this message is not changed while encrypted. Hence often a message authentication code is added to a ciphertext to ensure that changes to the ciphertext will be noted by the receiver. Message authentication codes can be constructed from symmetric ciphers (e.g. CBC-MAC).^{[citation needed]}

However, symmetric ciphers cannot be used for non-repudiation purposes except by involving additional parties.^[7] See the ISO/IEC 13888-2 standard.

Another application is to build hash functions from block ciphers. See one-way compression function for descriptions of several such methods.

Construction of symmetric ciphers[edit]

Many modern block ciphers are based on a construction proposed by Horst Feistel. Feistel's construction makes it possible to build invertible functions from other functions that are themselves not invertible.^{[citation needed]}

Security of symmetric ciphers[edit]

Symmetric ciphers have historically been susceptible to known-plaintext attacks, chosen-plaintext attacks, differential cryptanalysis and linear cryptanalysis. Careful construction of the functions for each round can greatly reduce the chances of a successful attack.^{[citation needed]}

Key management[edit]

Key establishment[edit]

Symmetric-key algorithms require both the sender and the recipient of a message to have the same secret key.All early cryptographic systems required one of those people to somehow receive a copy of that secret key over a physically secure channel.

Nearly all modern cryptographic systems still use symmetric-key algorithms internally to encrypt the bulk of the messages, but they eliminate the need for a physically secure channel by using Diffie–Hellman key exchange or some other public-key protocol to securely come to agreement on a fresh new secret key for each message (forward secrecy).

Key generation[edit]

When used with asymmetric ciphers for key transfer, pseudorandom key generators are nearly always used to generate the symmetric cipher session keys. However, lack of randomness in those generators or in their initialization vectors is disastrous and has led to cryptanalytic breaks in the past. Therefore, it is essential that an implementation use a source of high entropy for its initialization.^[8][9][10]

Reciprocal cipher[edit]

A reciprocal cipher is a cipher where, just as one enters the plaintext into the cryptography system to get the ciphertext, one could enter the ciphertext into the same place in the system to get the plaintext. A reciprocal cipher is also sometimes referred as self-reciprocal cipher.

Lack Of Randomness In The Key Generation Process 2

Practically all mechanical cipher machines implement a reciprocal cipher, a mathematical involution on each typed-in letter.Instead of designing two kinds of machines, one for encrypting and one for decrypting, all the machines can be identical and can be set up (keyed) the same way.^[11]

Examples of reciprocal ciphers include:

• Beaufort cipher^[12]
• Enigma machine^[13]
• Marie Antoinette and Axel von Fersen communicated with a self-reciprocal cipher.^[14]
• the Porta polyalphabetic cipher is self-reciprocal.^[15]
• Purple cipher^[16]

Practically all modern ciphers can be classified as either a stream cipher, most of which use a reciprocol XOR cipher combiner, or a block cipher, most of which use use Feistel cipher or Lai–Massey scheme with a reciprocal transformation in each round.

Notes[edit]

1. ^Other terms for symmetric-key encryption are secret-key, single-key, shared-key, one-key, and private-key encryption. Use of the last and first terms can create ambiguity with similar terminology used in public-key cryptography. Symmetric-key cryptography is to be contrasted with asymmetric-key cryptography.

References[edit]

1. ^Kartit, Zaid (February 2016). 'Applying Encryption Algorithms for Data Security in Cloud Storage, Kartit, et al'. Advances in ubiquitous networking: proceedings of UNet15: 147.
2. ^Delfs, Hans & Knebl, Helmut (2007). 'Symmetric-key encryption'. Introduction to cryptography: principles and applications. Springer. ISBN9783540492436.CS1 maint: uses authors parameter (link)
3. ^Mullen, Gary & Mummert, Carl (2007). Finite fields and applications. American Mathematical Society. p. 112. ISBN9780821844182.CS1 maint: uses authors parameter (link)
4. ^'Demystifying symmetric and asymmetric methods of encryption'. Cheap SSL Shop. 2017-09-28.
5. ^Pelzl & Paar (2010). Understanding Cryptography. Berlin: Springer-Verlag. p. 30.
6. ^Roeder, Tom. 'Symmetric-Key Cryptography'. www.cs.cornell.edu. Retrieved 2017-02-05.
7. ^14:00-17:00. 'ISO/IEC 13888-2:2010'. ISO. Retrieved 2020-02-04.
8. ^Ian Goldberg and David Wagner.'Randomness and the Netscape Browser'.January 1996 Dr. Dobb's Journal.quote:'it is vital that the secret keys be generated from an unpredictable random-number source.'
9. ^Thomas Ristenpart , Scott Yilek.'When Good Randomness Goes Bad: Virtual Machine Reset Vulnerabilities and Hedging Deployed Cryptography (2010)'CiteSeer^x: 10.1.1.183.3583quote from abstract:'Random number generators (RNGs) are consistently a weak link in the secure use of cryptography.'
10. ^'Symmetric Cryptography'. James. 2006-03-11.
11. ^Greg Goebel.'The Mechanization of Ciphers'.2018.
12. ^'.. the true Beaufort cipher. Notice that we have reciprocal encipherment; encipherment and decipherment are identically the same thing.'--Helen F. Gaines.'Cryptanalysis: A Study of Ciphers and Their Solution'.2014.p. 121.
13. ^Greg Goebel.'The Mechanization of Ciphers'.2018.
14. ^Friedrich L. Bauer.'Decrypted Secrets: Methods and Maxims of Cryptology'.2006.p. 144
15. ^David Salomon.'Coding for Data and Computer Communications'.2006.p. 245
16. ^Greg Goebel.'US Codebreakers In The Shadow Of War'.2018.

Lack Of Randomness In The Key Generation Process Theory